Electrostatic imaging
A new and general approach to the problem of Electrostatic Imaging (ESI) based on integral equations is under advanced investigation.
As is known, enjoying both an effective applicability to any electrically-reactive system and a dramatic instrumental simplicity with respect to more conventional imaging apparatuses, ESI is potentially useful in many different fields: volume imaging, proximity sensors, process and flow controls, geophysics, superconductivity, bioelectricity, material analysis, etc. .
Also the variety of names used to indicate what is basically the same technique is a proof about its wide circulation: ESI is named also ERT, Electrical Resistivity Tomography, or ET, Electrical Tomography, or EIT, Electrical Impedance Tomography, or EST, Electrostatic Tomography, or ECT, Electrical Capacitance Tomography, etc. .
So, from one side, the instrumental simplicity of ESI makes it highly advisable in very different experimental situations; otherwise, from the other side, just the countless number of names used to indicate what is basically the same technique assesses that the interpretation of collected data usually suffers the lack of a general theoretical picture.
This work arose from the need of a sound and unifying mathematical picture for ESI applied to reacting systems of very different nature in various experimental situations (e.g. process tracking in chemical reactors, the imaging of the combustion field in solid rocket propulsion, etc.). Therefore the maximum of generality in the theoretical picture is highly advisable.
The integral equations, derived in the scope of Potential Theory from Maxwell’s equations in quasi-static approximation, meet the requested generality. They establish a mathematical link which is both analytical and self-consistent (i.e. without any ad-hoc heuristic hypothesis) between the boundary-measured observables and the proper quantities which describe the behavior of any electrically-reactive contents inside the given finite volume.
If J is the total surface current-density, Φ the scalar electric potential, D the displacement vector (defined by:
![]() which enjoys the property:
which enjoys the property: ![]() , and where E is the electric field), the integral equations are:
, and where E is the electric field), the integral equations are:
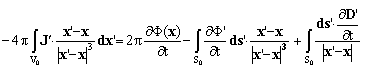
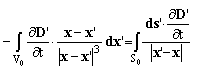
where ![]() ,
, ![]() and
and ![]() (see the figure). The R.H.S. of the equations contain only measurable quantities.
(see the figure). The R.H.S. of the equations contain only measurable quantities.
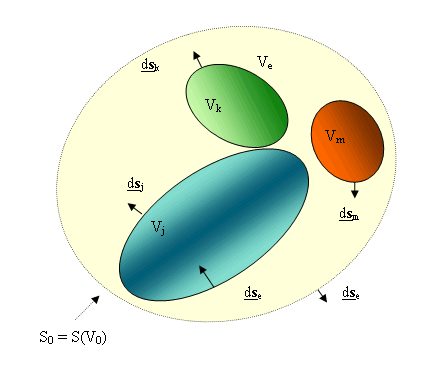
Note that two equations are required, since the presence of matter is usually related to the space- distribution of the electric conductivity σ and/or of the electric susceptibility ![]() .
.
Such integral equations act as a sound mathematical framework overcoming and unifying the many different approaches based on the numerical solution of the differential Dirichlet’s problem and the related approximations and improvements.
Moreover, by means of these integral equations, a self-consistent analysis about the various factors affecting the overall scope of any electrostatic imaging technique is allowed. This, in the author’s opinion, is the considerable usefulness of this work.
Indeed, the role of the electrode shapes, the competitive effect of macroscopic spurious couplings in their experimental layout, the effects of inclusions of any kind in the given volume, the theoretical space-resolving power, the reliability of any inversion method applied to the recovered experimental data, etc., can be directly discussed. So far, conventional numerical methods, although widely used, usually prevent from such a conceptually-simple and self-consistent approach, and are very far away from real experimental systems.
A comprehensive report, which both describes how these integral equations are obtained and discusses their scope, is in progress. It is worth observing that, in order to definitely asses either the reliability of the proposed mathematical picture or the feasibility of any electrostatic imaging technique, a careful theoretical investigation and a related considerable amount of experimental work are required. For instance, an effort is mandatory for evaluating the role of microscopic phenomena inside the given volume, or the presence of emf, or of pyroelectricity, or the existence of strong contents-wall interaction (at the electrode surfaces), etc.
Contacts
- Dr. Ubaldo Carretta, phone +39 02 66173 334

